Kai Washizaki

Involution: Inverting the Inherence of Convolution for Visual RecognitionをEfficientNetで試してみた

2021/03/25

Table of Contents

畳み込み演算の解析
Involution
Attention構造との比較
EfficientNetにInvolutionを導入し、実験してみた
まとめ

畳み込み演算の解析

まず、畳み込み演算について説明します。

高さ $H$ 、幅 $W$ 、チャンネル数 $C_i$ の特徴マップを $\mathbf{X} \in \mathbb{R}^{H×W×C_i}$ とし、各ピクセルでは、 $\mathbf{X}_{i,j} \in \mathbb{R}^{C_i}$ とします。また、 $K×K$ のカーネルを持つ $C_0$ 個の畳み込みフィルターを、 $\mathcal{F}_k \in \mathbb{R}^{C_i × K × K}, k=1, 2, \cdots, C_0$ とし、畳み込みカーネルは、 $\mathcal{F}_{k,c} \in \mathbb{R}^{K × K}, c=1, 2, \cdots, C_i$ とします。

このとき、各畳み込みフィルタに関する演算は、以下の式のように、各チャネルごとに畳み込みカーネルを積和演算したものになります。

\mathbf{Y}_{i, j, k} = \sum_{c=1}^{C_i} \sum_{(u, v) \in \Delta_K} \mathcal{F}_{k,c, u+\lfloor K/2 \rfloor, v+ \lfloor K/2 \rfloor} \mathbf{X}_{i+u, j+v,c}.

$\Delta_K$ は、中心画像に対する畳み込みを考慮した、近傍領域のオフセットであり、

\Delta_K = [\lfloor -K/2 \rfloor, \cdots, \lfloor -K/2 \rfloor × \lfloor -K/2 \rfloor, \cdots, \lfloor -K/2 \rfloor

の直積集合です。

また、ここでの、 $\lfloor x\rfloor$ は、床関数でx以下の最大の整数を表現しています。

上記の式から、チャンネルごとに異なるカーネルを使用している一方で、空間方向には同一のカーネルを使用してことが分かります。このことから、畳み込み演算には、空間にとらわれない特性と、チャンネル固有性という特徴があると言われています。

空間にとらわれない特性は、異なる場所で再利用することで畳み込みカーネルが効率的に適用できるようにし、カーネルによる変換がどの場所でも等価であることを追求しています。チャンネル固有性は、異なるチャンネルにおける多様な情報を収集するために必要とされています。

実際、最新のニューラルネットでは、VGGNetの登場以降、畳み込みカーネルを3x3以下に制限することがデファクトスタンダードになっており、実際に性能が向上しています。

これらのことから、変換の等価性の向上が性能向上に寄与し、一方で、空間的位置に関する多様な視覚パターンに適応する能力が低くなっているとも言われています。 ImageNet-trained CNNs are biased towards texture; increasing shape bias improves accuracy and robustnessでは、画像認識モデルが形状よりテクスチャを優先して認識するということが指摘されていました。例えば、下図のように猫の形状で象の皮膚テクスチャの画像を認識させた時、テクスチャにより象と認識しています。

誤った画像認識

また、各チャンネルに対応する畳み込みカーネルの重みは、Speeding up Convolutional Neural Networks with Low Rank Expansionsにて高い冗長性を持つと言われており、これは学習後にカーネルの削減など圧縮が可能であることからも分かります。

Involution

論文では、畳み込み演算の欠点に対して、空間的に特異であり、チャンネルに依存しないという特徴を持つInvolutionカーネル $\mathcal{H} \in \mathbf{R}^{H × W × K × K × G}$ を提案しています。

Involution カーネル $\mathcal{H}_{i, j, ., .,g} \in \mathbf{R}^{K×K}, g = 1, 2, \cdots, G$ は、特徴マップの座標 $(i, j)$ におけるピクセル $X_{i,j} \in \mathbf{R}^C$ に対して演算され、一方で、チャンネル間では、共有のカーネルで演算します。

以下に、特徴マップに対するIvolutionカーネルの積和演算の式を示します。

\mathbb{Y}_{i,j,k} = \sum_{(u, v) \in \Delta_K} \mathcal{H}_{i,j, u+ \lfloor K/2 \rfloor, v + \lfloor K/2 \rfloor , \lceil kG/C \rceil} X_{i+u, j+v, k}

式の通り、 $kG/C$ から、チャンネルを $G$ 分割し、分割したチャンネル間ではカーネルを共有していることが分かります。

実装上、あるピクセル $(i,j)$ に対するIvolutionカーネルは、以下のように設計されています。

\mathcal{H}_{i,j} = \mathbf{W_1} \sigma (\mathbf{W}_0 \mathbf{X}_{i,j})

$\mathbf{W}_0 \in \mathbb{R}^{C/r ×C}$ , $\mathbf{W}_1 \in \mathbb{R}^{(K×K×G) × C/r}$ は、線形変換です。 $r$ は、減衰比です。 $\sigma$ は、バッチ正規化と非線形活性化関数を暗に示しています。

実際、論文では、Resnetに適用し、Bottleneck部分の3×3のConvolution部分をInvolutionに変更し、

Conv2d(kernelsize=1) + BatchNorm + Relu
Involution() + BatchNorm + Relu
Conv2d(kernelsize=1) + BatchNorm

という処理の実装が行わたRedNetとして提案されていました。

空間情報とチャネル情報が混ざり合うと、ニューラルネットワークで、重い冗長性が生じる傾向があり性能が低くなると言われています。しかし、上記のような実装構造にすることで、チャンネル-空間、空間単独、チャンネル単独のように情報の相互作用を上手く切り離したため精度が良かったと言われていました。特に、1×1の畳み込みがチャネル情報の交換には重要とも強調されていました。

個人的には、Involutionでも、チャンネルを $G$ 個に分割している時点で、チャンネル間の相互作用が発生するのではと思ったのですが、論文では、空間単独に作用する処理とのことでした。

Attention構造との比較

論文では、Involutionカーネルは、本質的にはSelf-Attentionの一般化したバージョンとしています。

Self-Attentionは、入力 $\mathbf{X}$ の線形変換より得られるQuery $\mathbf{Q}$ , Key $\mathbf{K}$ , Value $\mathbf{V}$ を用いて、

\mathbf{Y}_{i,j,k} = \sum_{(p,q) \in \Omega} (\mathbf{Q}\mathbf{K}^T)_{i,j,p,q, \lceil kH/C \rceil} V_{p,q,k},

の式で表すことができます。 $H$ は、multi-head self-attentionのheadの数です。

Involutionとの類似点は、加重和を用いて、近傍のピクセル $\Delta$ 、または、それ以下の範囲のピクセル $\Omega$ を収集することです。ここでの、 $\mathbf{Q}\mathbf{K}^T$ が、Involutionカーネルに相当するものです。Involutionカーネルとは異なり、特定のピクセル( $i,j$ )だけでなく、近傍のピクセルの情報から決定するカーネルになっています。

では、なぜInvolutionカーネルはピクセル間の関係を記述していないにもかかわらず、相対的な位置関係を学習できていると言えるのでしょうか？

RedNetは、Attentionを用いた重度な空間関係ベースのモデルと同等の精度を出しており、このことから、空間情報の表現学習が上手くいっていることが分かる
Stand-Alone Self-Attention in Vision Modelsにて、 $\mathbf{K}$ を位置エンコーディングに置き換えても、モデルの性能が低下しないことが発表されている

特に2番は重要だと思います。 $\mathbf{Q}\mathbf{K}^T$ でピクセル間の関係を明示的に記述することなく、視覚タスクで性能が低下しないということは、カーネルの出力に暗黙的に相対的な位置情報が組み込まれているのではないかと考えられます。

また性能の比較したとき、Self-Attentionに基づくモデルの性能は、多種類の視覚タスクに対応する汎用性を示すことができていない、一方で、Involutionは、多種多様なタスク(画像分類、物体検出、セマンティックセグメンテーション)に対応できています。

EfficientNetにInvolutionを導入し、実験してみた

論文中では、ResNetにInvolutionを導入したRedNetを提案していました。そのまま実験しても面白くないので、EfficientNet B0にInvolutionを導入して実験してみました。

Involutionの実装は、公式の実装がOpenMMLab仕様になっており、かなりチューニングされていたので、Non-Officialですが、ChristophReich1996 / Involutionを参考にしました。論文にも、Pytorch-likeな疑似コードが掲載されており、それとほとんど同じです。

疑似コード

EfficientNet B0の基本構造は、以下の図のとおりです。

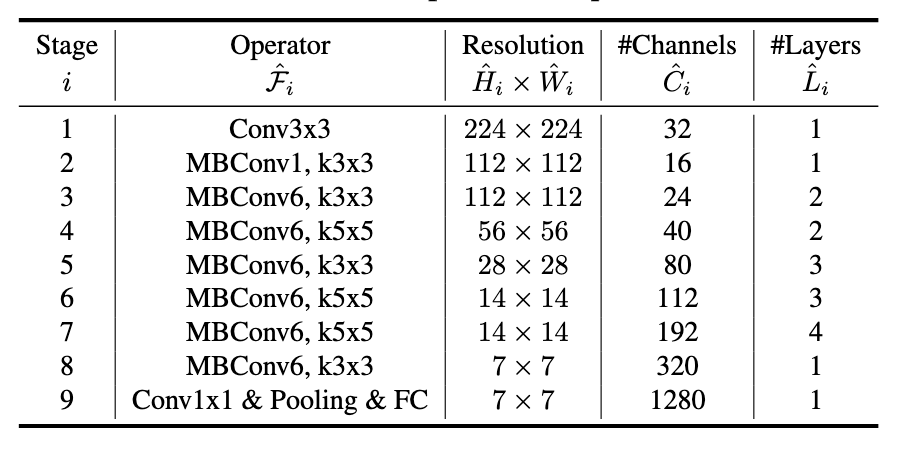
efficient_net_b0

BMConvモジュールは、基本的に以下の構造となっています。（引数などは簡略化のため書いてません）

# ConvModule
out = Conv2d(inuput)
out = nn.BatchNormalization(out)

# activatoin
out = Swish(out) 

# Squeeze Excitation
tmp_out = nn.Sequential(
            nn.AdaptiveAvgPool2d(1),
            nn.Conv2d(),
            Swish(),
            nn.Conv2d(),
        )(out)
out = out * torch.sigmoid(tmp_out)

# ConvModule
out = Conv2d(inuput) # 1x1 conv
out = nn.BatchNormalization(out)

今回の実験では、Squeeze Excitation部分をInvolutionに変更してみました。

Involutionのパラメータは、以下のようにしています。

param	value
$G$	4
r	4
K	7

学習の設定は以下の通りです。

param	value
Optimizer	AdamW
スケジューラー	ReduceLROnPlateau
lr	0.25
バッチサイズ	10

学習は、スケジューラのPARTIENCEを10として、学習が進まなくなるまで行っています。

データセットは、Intel Image Classificationを用いました。建物や山,海など風景が対象のデータセットになります。

dataset

実験0 - EfficientNetを学習させてみた

EfficientNetのB0, B4を学習させました。

model	params (M)	acc
b0	4	82.8%
b4	17.2	86.9%

まずまずの精度です。Kaggleに載っている結果と比較すると低いので、チューニングが必要かもしれませんし、実装が間違っているかもしれませんが、今回は、この値を参考値として使用します。

実験１ - Squeeze Excitation -> Involution

まず、単純にSqueeze ExcitationをInvolutionに変更しました。

out = ConvModule(out)
out = Swish(out) 

out = Involution(out)

out = ConvModule(out)

実験結果としては、Acc 17%で、全く学習が上手くいきませんでした。

model	params (M)	acc
実験1	5.7	17.0%

実験2 - BatchNorm + Swishの追加

次に、BatchNormalizationと活性化関数(Swish)を追加しました。これは、論文の実装にかなり似た形式になっています。

out = ConvModule(out)
out = Swish(out) 

out = Involution(out)
out = nn.BatchNormalization(out)
out = Swish(out) 

out = ConvModule(out)

結果は、まずまずといったところですが、学習ができていることが、確認できました。

model	params (M)	acc
実験2	5.7	77.0%

実験3 - EfficientNetのStage(7, 8)を削除

Self-Attentionを用いたモデルは、大量のデータが必要で学習が遅いという欠点があります。そこで、Involutionを用いたモデルも学習が遅いのではと思い、思い切ってEfficientNetの層を削除しました。

実験2までの工夫に加えて、Efficinet b0の概要図のstage6, 7を削除し学習させました。ここで、今までの実験で最高性能が出ました。

model	params (M)	acc
実験3	1.5	89.0%

実験4 - EfficientNetのStage(6, 7, 8)をさらに削除

実験2までの工夫に加えて、実験3よりさらに多いEfficinet b0のstage5, 6, 7を削除し学習させました。パラメータを削除しすぎたのか、性能が下がりました。

model	params (M)	acc
実験4	0.6	84.3%

実験5 - 実験3の条件に加えて、畳み込み部分のカーネルサイズを全て1に変更

提案手法である、RedNet似合わせるため、Involutionの前後にある畳み込みのカーネルサイズを1にしました。カーネルサイズを1にした部分は、Involution演算の直前の畳み込み演算です。Involution後の畳み込み演算は、もともとEfficientNetでもカーネルサイズ１に設定されていました。

これも、あまり精度が出ませんでした。論文とは反対に、Involution前の畳み込みはカーネルサイズが大きい方が精度が良いという結果になりました。

model	params (M)	acc
実験5	1.4	81.4%

実験を経て

実験の結果を以下に再掲します。実験３の結果は、モデルのパラメータ数がかなり少ない中、実験の中で最大の精度となりました。この結果には、かなり驚きを得ています。

model	params (M)	acc
実験0 - EfficientNet b0	4	82.8%
実験0 - EfficientNet b4	17.2	86.9%
実験1 - Involutionに変更	5.7	17.0%
実験2 - Involution + BN + Swish	5.7	77.0%
実験3 - Involution + BN + Swish + Stage(7, 8)削除	1.5	89.0%
実験4 - Involution + BN + Swish + Stage(6, 7, 8)削除	0.6	84.3%
実験5 - Involution + BN + Swish + Stage(7, 8)削除 + 畳み込みカーネルサイズ1に変更	1.4	81.4%

実験1, 実験2を経て、Involution、BatchNormalization、活性化関数という構造がInvolutionの学習において重要であると分かります。

実験3, 4では、モデルのDepthを小さくしています。適切なDepthの設定が重要であることが分かります。畳み込みを用いたときは、一般的には、Depthを深くしたら精度が良くなりますが、実験3にて、逆にDepthを小さくしたら、最も精度が良くなりました。

DeepViT: Towards Deeper Vision Transformerという論文では、Attention構造を持つVision transformersの深い層で、特徴マップが類似する傾向があり、表現学習のための効果的な概念の獲得を妨げているという指摘がありました。DeepVitの論文と今回の実験に用いたEfficientNetのDepthのスケールは異なりますが、深い層で精度がでなかった原因の一つかもしれません。

また、実験5にて、論文で良好な結果を得るためのTipsとして書かれていた、Involution前後の畳み込み演算のカーネルサイズを1にするという変更を行いましたが、良好な精度が得られませんでした。今回は、Toy実験で、論文ほど正確に実験できているとは思っていませんが、今回のような例がでているので、Involutionに関しては、より調査が必要かもしれません。

まとめ

今回は、EfficientNetにInvolutoinを導入し、実際に実験してみました。実際の研究同様に大きなデータセットを使用し、しっかりとパラメータチューニングをやるなど細かな対応はできていませんが、今後の参考になる考察ができたと思っています。

Involutionは、ViTのようなAttentionベースのモデルよりは扱いやすいと思います。一方で、畳み込み演算に取って代わるかというと、今後に期待という状態です。論文では、ResNetに対してInvolutionを導入していましたが、他のモデルへ導入した時の挙動に関する研究など、今後より研究されることで、畳み込みと同様に、視覚タスクで一般的に使用される演算の一つになるとことが楽しみです。