Table of Contents
Most-Popular推薦を実装して理解する
こんにちは。塚本です。 現在、社内で推薦システム: 統計的機械学習の理論と実践 | Agarwal, Deepak K., Chen, Bee‐Chung, 直希, 島田, 健志, 大浦 |本 | 通販 | Amazonの本を輪読しています。
ようやく、6章の内容が終わり、具体的な話になってきました。
そろそろ実装をして理解しようというモチベーションです。
Most-Popular推薦
この推薦手法はクリック率(CTR)などの肯定的なアクションにもとづいて、アイテムをスコアリングし、そのスコアの高いアイテムから順に提供していくシンプルな推薦手法です。
実際によく使われるアプローチは、CTRの上位個のアイテムを推薦していくことです。
全体の傾向から単純にCTRの多い商品をおすすめに表示するなどがこれに当たります。
それぞれのユーザーがそれぞれのアイテムに対して、どのような反応をしめしたかなど、個別の推薦を求めないものに対しては役に立つようです。
問題定義
まず、Most-Popular推薦を定式化します。
をアイテム集合、を時間とします。
このとき、をアイテム、を時点、をにおけるのCTRと表すこととします。
が既知であれば、時点における最適な推薦戦略は、すべてのユーザーに対して、アイテム
を提供することとなります。
簡単に言うと、最も人気のある(最もCTRの高い)アイテムをユーザーへ提供し続ける戦略です。
これを行うため、時間ごとにかわるアイテムのCTRを追従して行かなければなりません。
今回はベイズ的手法の一つとしてはGamma-Poissonモデルを利用します。
時点におけるCTRを、クリック数を、閲覧数をとした時
- 平均の時の、クリック数をからサンプリング
- 事前分布として、[過去に観測されたクリック数, 過去に観測されたビュー数]として、平均をもつを仮定
- の事後分布として、を得る
これで更新し、アイテムのCTRの追従していきます。
加えて、時間ごとに割引率をきめるDynamic Gamma-Poissonモデルとの比較も実験してみましょう。
実装
まずは通常のGamma-Poissonモデルを実装します。
import math
import matplotlib.animation as animation
import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import gamma, poisson
# input
p = 0.6
N = 10
# parameters
a = 0
g = 0
step = 50
xs = np.arange(0.01, 1.0, 0.01)
plot_gif = []
fig = plt.figure()
def update(frame):
global p, a, g
plt.cla()
if frame == step / 2:
p /= 2
click_dist = poisson(p * N)
c = click_dist.rvs()
a = a + c
g = g + N
posterior_dist = gamma(a, scale=1./g)
y = [posterior_dist.pdf(x) for x in xs]
img = plt.plot(xs, y, "r")
plt.title('E[p_t]={}'.format(
str(math.floor(a / g * 100) / 100).ljust(4, '0')))
plt.xlim(0, 1)
plt.ylim(0, 15)
plot_gif.append(img)
ani = animation.FuncAnimation(fig, update, frames=step)
ani.save('image.gif')
上記実行結果は以下となります。
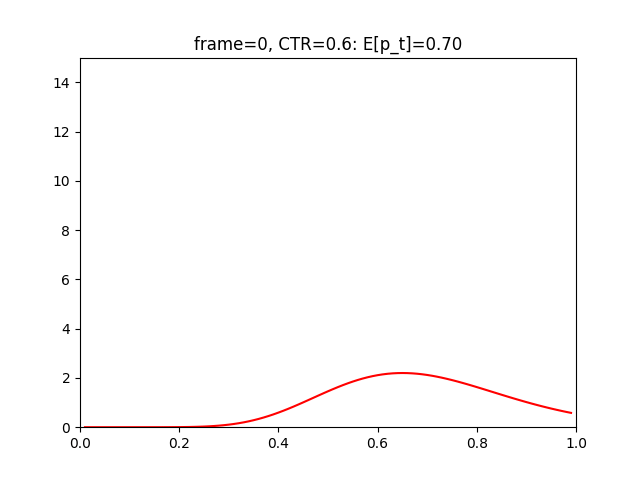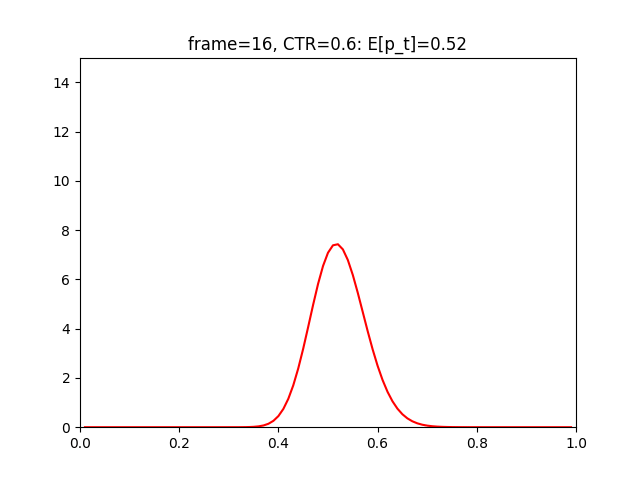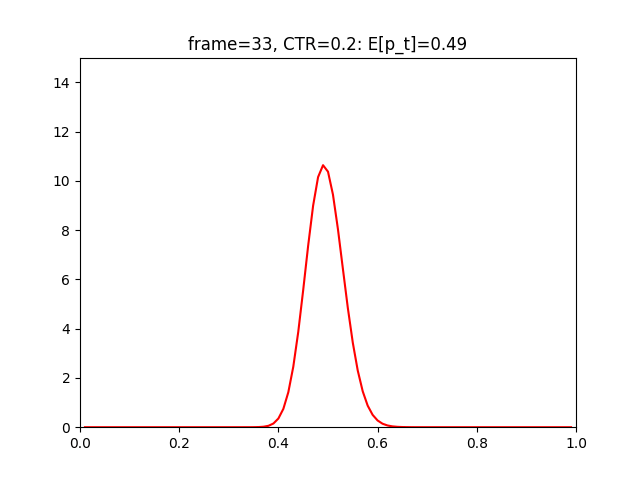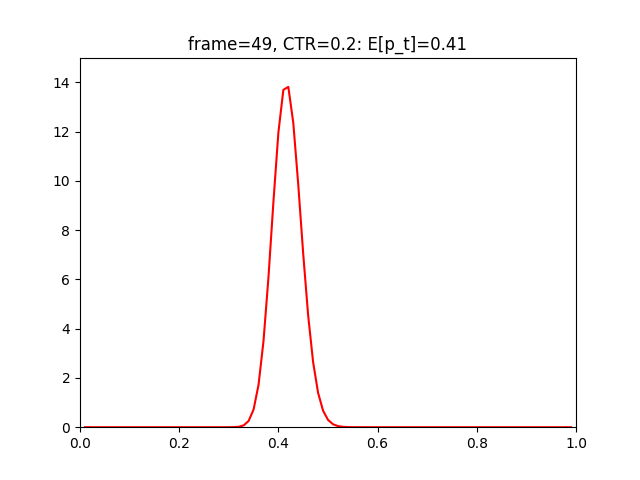
実行されるたびに、CTRの値がだいぶ確信的になっています。
次に、Dynamic Gamma-Poisson分布について記載します。
import math
import matplotlib.animation as animation
import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import gamma, poisson
# input
p1 = 0.6
p2 = 0.2
N = 10
w = 0.95
# parameters
a = 0
g = 0
step = 50
xs = np.arange(0.01, 1.0, 0.01)
fig = plt.figure()
def update(frame):
global a, g
plt.cla()
if frame <= step / 2:
p = p1
else:
p = p2
click_dist = poisson(p * N)
c = click_dist.rvs()
a = w * a + c
g = w * g + N
posterior_dist = gamma(a, scale=1./g)
y = [posterior_dist.pdf(x) for x in xs]
plt.plot(xs, y, "r")
E = math.floor(a / g * 100) / 100
plt.title('frame={}'.format(frame) + ', ' +
'CTR={}'.format(p) + ': ' +
'E[p_t]={}'.format(str(E).ljust(4, '0')),
)
plt.xlim(0, 1)
plt.ylim(0, 15)
ani = animation.FuncAnimation(fig, update, frames=step)
ani.save('dgp.gif')
通常のGamma-Poissonモデルと比べてみましょう。
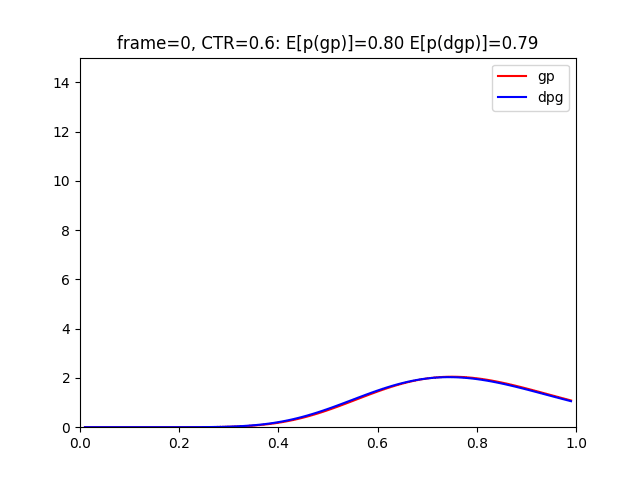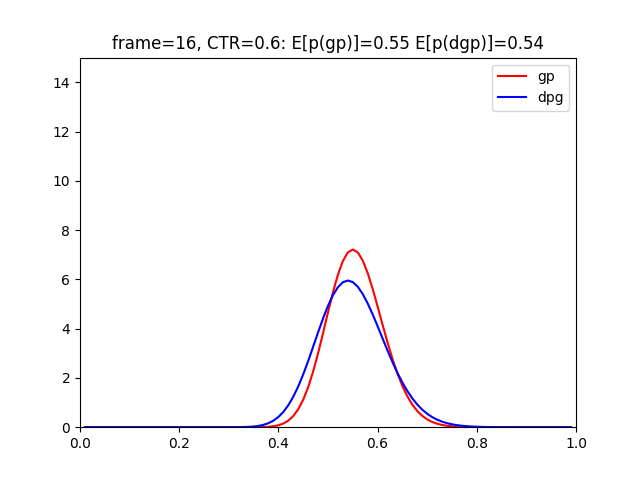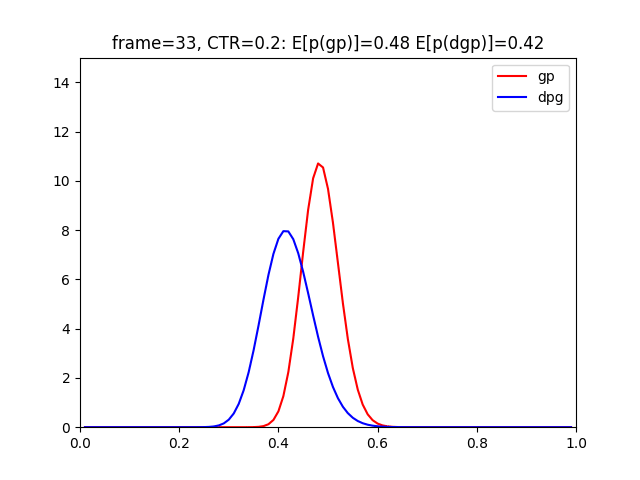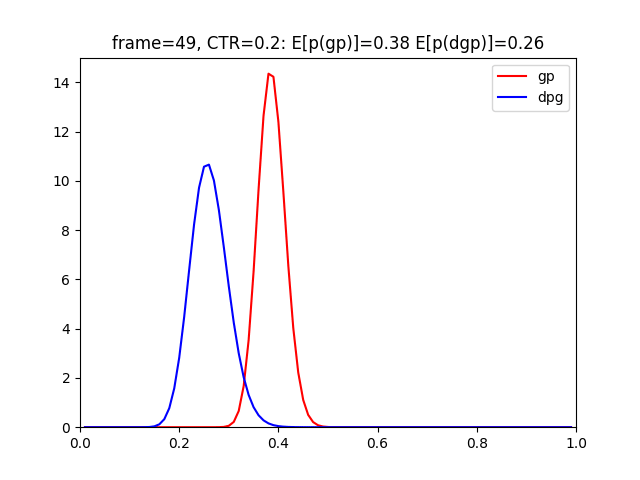
青ラベルがDynamic Gamma-Poissonモデルとなっています。
コードをみてもらえるとわかると思いますが、のバイアスをかけて、前回までの結果を割り引いています。
グラフからもわかる様に、赤のグラフよりも早くCTR=0.2へ追従できていますね。
これは、前回までの結果に引っ張られすぎないということが原因となっています。
2つのアイテム、2つの時点
前述までは、1つのアイテムのみでしか考えていませんでした。
通常は複数アイテムと相対して、推薦しますよね。
ここでは、簡単に2つのアイテムと2つの時点でのみ考えてみます。
以下の条件を元に議論をすすめます。
1つのアイテムのCTRは既知であると仮定し、そのアイテムを、CTRが未知のアイテムをとします。
2つのアイテムしか考えないので、以下で定義。
- : それぞれ時点0、および時点1におけるユーザの訪問数
- : それぞれ時点0、および時点1のアイテムのCTR
- : それぞれ時点0、および時点1のアイテムのCTR
- : それぞれ、アイテムにおける、時点0と1でのユーザー訪問数
- : アイテムの時点0でのクリック数
- かつ
ベイズ最適戦略では、クリック数の期待値を最大化することが目的となってきます。
この問題の場合、クリック数を最大にするときのの値を求めるのが目的です。
を最大にすることを考えることになります。
上記式を整理すると以下。
この部分を実装を書くと以下の感じになりました。
import math
import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import gamma, poisson
# parameters
E_p0 = 0.088
g = 500
a = E_p0 * g
N_0 = 2000
N_1 = 40000
q_0 = 0.1
q_1 = 0.1
prior_dist = gamma(a, scale=1./g)
p_0 = prior_dist.rvs()
print(p_0)
xs = np.arange(0, 1.0, 0.01)
ys = []
for x in xs:
click_dist = poisson(p_0 * x * N_0)
c = click_dist.rvs()
a = a + c
g = g + N_0 * x
gain = N_0 * x * (E_p0 - q_0) + N_1 * max(a/g - q_1, 0)
E_clicks = gain + q_0 * N_0 + q_1 * N_1
ys.append(E_clicks)
plt.title("p_0 = {}".format(math.floor(p_0 * 1000) / 1000) + ' ' +
"q_0 = q_1 = {}".format(q_0) + ' '
"E[p0] = {}".format(E_p0)
)
plt.xlabel('x')
plt.ylabel('E[#clicks]')
plt.plot(xs, ys, 'r')
plt.savefig("2x2problem.png")
結果↓
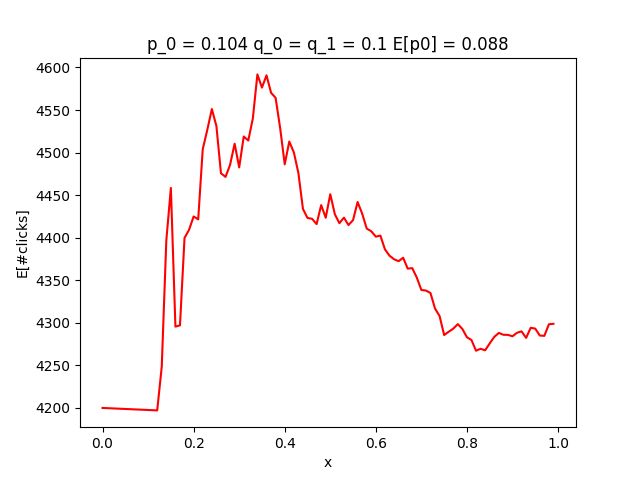
この場合、だいたい0.4あたりで最大を取っています。
ということなので、大体0.4の割合でアイテムを表示したら良いと言うことになります。
本来、このの値を解析的に求める方法がありますが(本書にも書かれてます)、これを書くと長くなるので省略。
おわりに
続きは、複数のアイテムでも適切な推薦ができるように実行するというフェーズになっていきます。
推薦方法はMost-Popularの他にもあるので、かけたらまたこうやって実装して理解したいと思います。
理解したと言えるのはコードに落としたとき(具体物に表現できたとき)だと個人的に思ってるので、とても良い機会だと思いました。

Tsukamoto Makoto
Company: Fusic CO., LTD. お仕事はRuby 趣味ではJulia jl.devというJuliaのユーザーグループの管理人しています。Juliaが好きな方は是非に〜