Table of Contents
こんにちは、鷲崎です。先日(21年6月6日)、「○○ is Not All You Need」系の論文の系譜であるTabular Data: Deep Learning is Not All You Needという研究が発表されました。この研究では、表形式のデータにおいて、XGBoostの精度が深層ニューラルネットワークを上回ることが分かったと主張されていました。確かに、KaggleでもXGBoostは頻繁に使用されますし、チューニングの必要性がないことも嬉しいとこです。
しかし、この2日前(21年6月4日)に、表形式のデータで、競争力ある新たな深層学習アーキテクチャである、Self-Attention Between Datapoints: Going Beyond Individual Input-Output Pairs in Deep Learningという研究が発表されていました。下図(論文中Table 1)は、UCIベンチマークを用いて、左から2値分類、多クラス分類、回帰のタスクで性能を比較したものです。論文にて提案されているNon-Parametric Transformers (NPTs)は、Boosting系の手法と比較しても同等以上の結果を示しています。
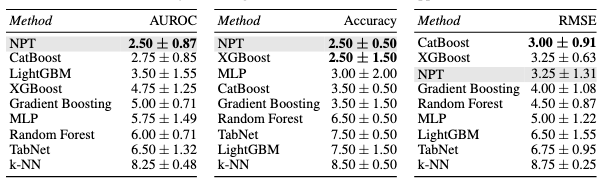
本記事では、この深層学習において新しい考え方であるSelf-Attention Between Datapointsを解説します。
何が新しいのか??
下図(論文中Figure 1)が、提案手法(NPTs)の概要です。
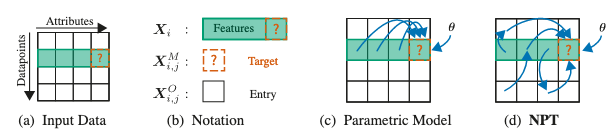
入力データ(a)は、属性とデータ点からなります。例えば、属性は、性別、所属などの特徴に関する軸で、データ点は文章1, 文章2などデータごとの軸です。
(b)は、学習や予測に使用するデータに関する図で、は、あるデータ点における特徴量です。は、予測したいデータ点のある特徴のことです。はデータ全体のなかのある点のことです。
(c), (d)は、それぞれ、パラメトリックなモデルと、論文で提案しているNPTsを表現しています。
一般的な教師あり学習は、CNNやTransformersなどのパラメトリックなモデルに依存しています。図の通り、パラメトリックなモデルは、データ点間の直接的な依存関係は考慮しておらず、あるデータ点の情報を用いた予測になります。
論文で提案されているNPTsは、予測時に同じデータ点だけでなく、データ全体(学習データも含む)を使用しています。これは、とても柔軟性のあるモデルが必要で、データ点間の相互作用を明示的に学習して予測を行う手法になっています。また、このように学習データとの関係性もモデル化して予測を行うモデルが、ノンパラメトリックなモデルと呼ばているため、Non-Parametric Transformersと名付けられています。
では、NPTsは、今までのノンパラメトリックな手法と、どのように異なるのでしょうか? ガウス過程などの従来のノンパラメトリックな手法は、入力データ間の相互作用がアーキテクチャの選択とハイパーパラメータによって完全に決定されてしまうという、データに対する柔軟性の制限があります。また、深層ニューラルネットワークを用いた手法も、NPTsと比較して、確率過程に大きく依存しており、柔軟性に欠け、データに強い過程が必要になります。
NPTsは、図(d)のようなデータ点間の関係をTransformerを用いて明示的(直接的)に学習することで、予測性能を改善しています。
Non-Parametric Transformers (NPTs)
NPTsは、(1)入力データ, (2)self-attentionによるモデル化, (3)マスキング の3つから構成されます。これらの要素の概要図(論文中Figure 2)は、以下のようになっています。
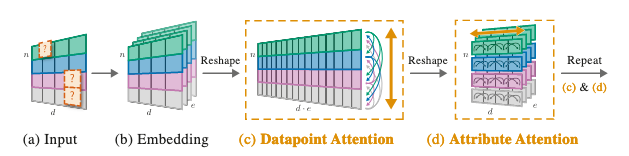
(1) 入力データ
上図(a)のように入力データは、です。がデータ点の数で、が属性の数です。
例えば、回帰タスクの場合、入力データをとし、予測対象であるラベルの属性を最後の属性とすることで予測可能になります。
このように、NPTsでは、予測ターゲットをマスクする自然言語処理のMasked Language Modelingのような処理を行います。そのため、でマスクを表現したバイナリ行列を用いて、入力値から予測値を予測するタスクを解くことになります。
(2) self-attentionによるモデル化
上図(c), (d)のself-attentionによるモデル化の部分を解説します。
まず、(b)のように、(c)に対する入力データを形成します。これは、最初の入力データに対して、各データ点ごとに線形埋め込みを行い結合したものです。
(c)では、入力データに対して、データ点間の関係性を捉えるようにMulti-head self-attention(MHSA)を適用ています。そして、(d)では、属性間の関係性を捉えるようにMHSAを適用しています。これを繰り返すことで学習しています。
MHSAに関する詳細は、ここでは省きますが、という関数でMHSAが適用されるとします。
(c), (d)に関して、具体的な処理方法を説明します。まず、(c)データ点間の関係性を捉えるAttentionです。(c)では、入力をに変形し、を計算しています。その後、に変形しています。
(d)属性間の関係性を捉えるAttentionは、(c)の出力の各データ点を入力として、各データ点にMHSAを行い結合するにより計算できます。
(3) マスキング
マスキングに関して解説します。学習に使用するマスクは、特徴マスクとターゲットマスクです。特徴マスクは、から、確率的に選択されます。ターゲットマスクは、訓練ラベルから確率的に選択されます。これらのマスクの予測損失は、対数尤度で与えられ、ハイパーパラメータを用いて、で与えられます。テスト時には、テストに使用するデータ点におけるターゲット部分をマスクするのみです。
学習時に属性もマスクする理由としては、データセット全体の表現学習を促すためです。タスクの難易度が上がり、有益な正則化の効果があるとのことです。
まとめ
本記事では、NPTsの手法に関して解説しました。実験の結果は、記事の最初に示した図の通りでした。記事で詳細な解説は行っていませんが、論文には、実際に実装する際にデータセットが大きすぎる時の対処法や、データ点間のAttentionに関する議論などが記載されています。
今回、表形式のデータに関する新たなアーキテクチャであるNPTsに関して説明しましが、まだまだ、ノンパラメトリックな手法の欠点であるスケーリングの限界や計算が重いなど改善すべきところは、多くあります。今後、使われていくのか、使われないのか未知ですが、個人的には、Kaggleなどで使われはじめたら、使っていきたいですね。
深層ニューラルネットワークが表形式のデータで競争力がないと言われている中、同時に新しい手法が出てくる、この深層学習界隈のカオスでスピード感のある発展を面白く思います。
