Table of Contents
こんにちは、鷲崎です。2020年、新しい3次元空間の表現手法として、Neural Radiance Fields(NeRF)が登場しました。この手法は、下図のように複数の画像からNeRFを学習することで、任意の視点(位置と角度)から見えるである画像を表現できるようになります。
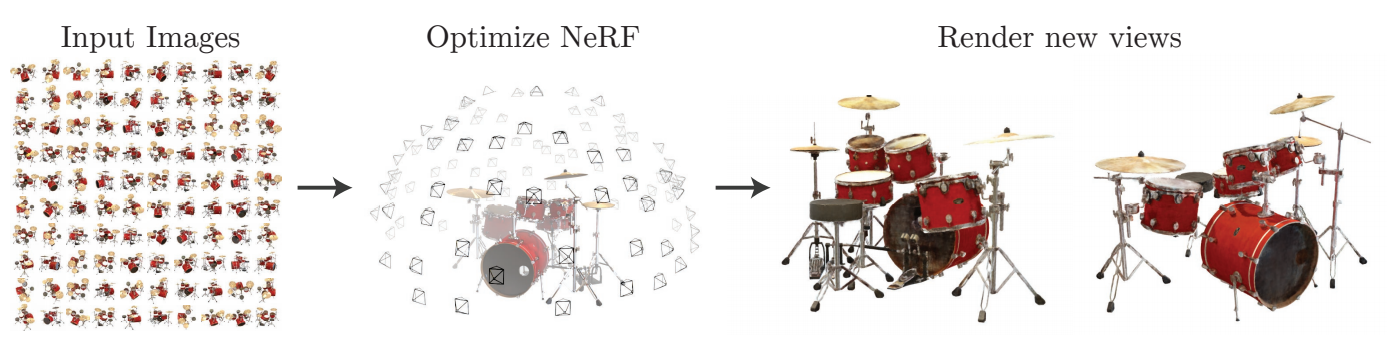
この手法の面白いところは、学習に使用した画像の中に存在しない新しい視点の画像が生成できることです。そのため、以下の動画(論文公式ページより参照)のように滑らかな視点変化の作成もできます。

また、NeRFは、3D空間をニューラルネットワークで表現できるので、より研究が進めば、SLAMなどロボット研究の進歩につながるのではと期待しています。
NeRF
実際、NeRFは、画像を表現しているわけではありません。Radiance Fieldsと言う、ある点の物体の色と密度をニューラルネットワークで表現しており、これを基に画像が生成されています。
NeRFの詳細に関しては、弊社機械学習チームの濱野が書いた記事や、【論文読解】NeRF in the Wild: Neural Radiance Fields for Unconstrained Photo Collectionsなど、わかりやす記事が多く書かれているので参考にしてください。
NeRFの欠点
一般的に、インターネット上に公開されている動画は、人間や動物、車などの多様な動的なコンテンツを含んでいます。しかし、NeRFを表現する手法の多くは、学習するシーンが静的であることを仮定しています。そのため、下図の右端のように動的な物体を含む動画では、不確かなNeRFを獲得してしまい、適用が困難です。
そこで、空間に加え時間方向も表現したNeural Scene Flow Fields (NSFF)が提案されました。

NSFFを実際に試してみました!
空間に加え時間方向も表現したNSFFの詳細な解説の前に、どんな手法であるかイメージを持ってもらうため、実際に試してみた結果を紹介したいと思います!
学習に使用した動画は、以下のものになります。

この動画から、10FPSで画像を切り出し、それを学習データとして使用しました。
学習には、この動画の他に、カメラパラメータと言われる撮影条件のようなものが必要になります。これは、COLMAPという、複数の画像から3Dモデルを作成する三次元再構成ライブラリを用いて取得します。COLMAPにより今回の動画から得られる3Dモデルは、以下のようなものになりました。
机の上の静的な物体は、3Dモデルになっていますが、人物やモニターなど動いているものは、あまり結果がよくありませんでした。
さて、COLMAPにより取得した複数枚の画像とカメラパラメータを用いて、オフィシャルのコードを参考にしつつ、NSFFを学習させてみました。学習には、GeForce RTX 3090を使用したのですが、4日ほどかかりました。結果は、下の動画のようになり、かなり良い結果が得られていると思います。 視点を固定したり、同じ視点付近で視点を回転させています。もっと動きがあれば、分かりやすいかもしれませんが、再度、別の動画で学習労力がありませんでした。公式のサイトでは、より面白い動画を見ることができます。
では、解説パートに移りたいと思います。
NSFFとは?
論文中には、「動的なシーンを空間と時間の連続した関数として表現し、その色と密度だけでなく、3Dシーンの動きも含まれていること」を提案したと書かれています。つまりNSFFの概念としては、NeRFに時間方向の情報を加えたものになります。
そして、特に重要な提案部分は、手法の名前にもなっている3Dの密なScene Flow Fieldsをモデル化することです。このモデル化により、空間と時間の両方の変化に対して補間することを可能にしています。一方で、このモデル化は、かなりチャレンジングな問題で、レンダリング品質を向上するために、様々な工夫が行われています。
動的な環境におけるScene Flow Fields
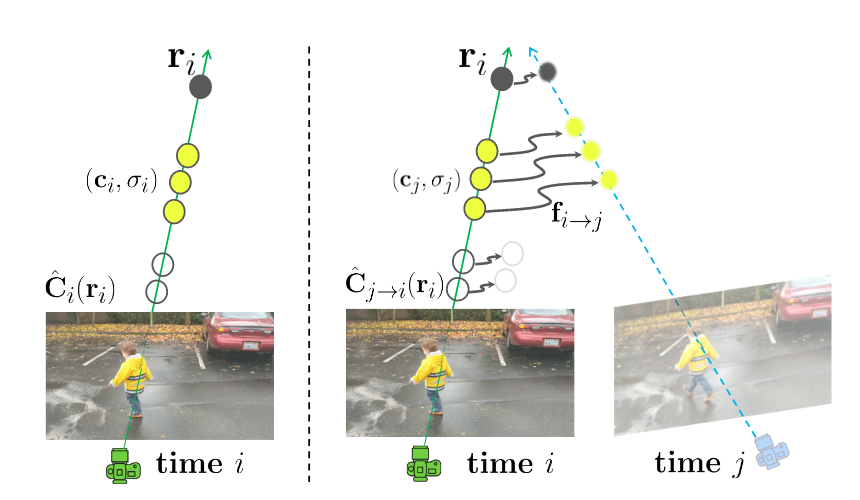
下図は、Scene flow fieldsの概要図(論文中Fig.2)です。ある時刻において、あるピクセルの色()を考えたとき、カメラ中心からそのピクセルを通る線をベクトルで表現しています。そして、そのベクトル上の3次元の点は色と密度で表現されています。
時刻において、あるピクセルに先ほど考えた時刻のピクセルと同じものが写っているとすると、上に同じ色と密度の点が存在すると考えられます。そのため、上で、時刻における色と密度に一致する点を探索することで、色と密度の位置を推測できます。
このとき、時刻からで、3次元空間を移動した点の移動量をScene flow と言います。もし、静的な物体だと、移動しないのでScene flowは小さいです。一方で、動的な物体は、時刻と共に変化するので、Scene flowも大きくなります。
実際の処理では、時刻に対応したScene Flowとして時刻と時刻のものを計算します。
Scene Flow の最適化
Scene Flowの損失関数は、多くの曖昧さに対応するため、以下のような3つの工夫により構成されています。
- 輝度一貫性
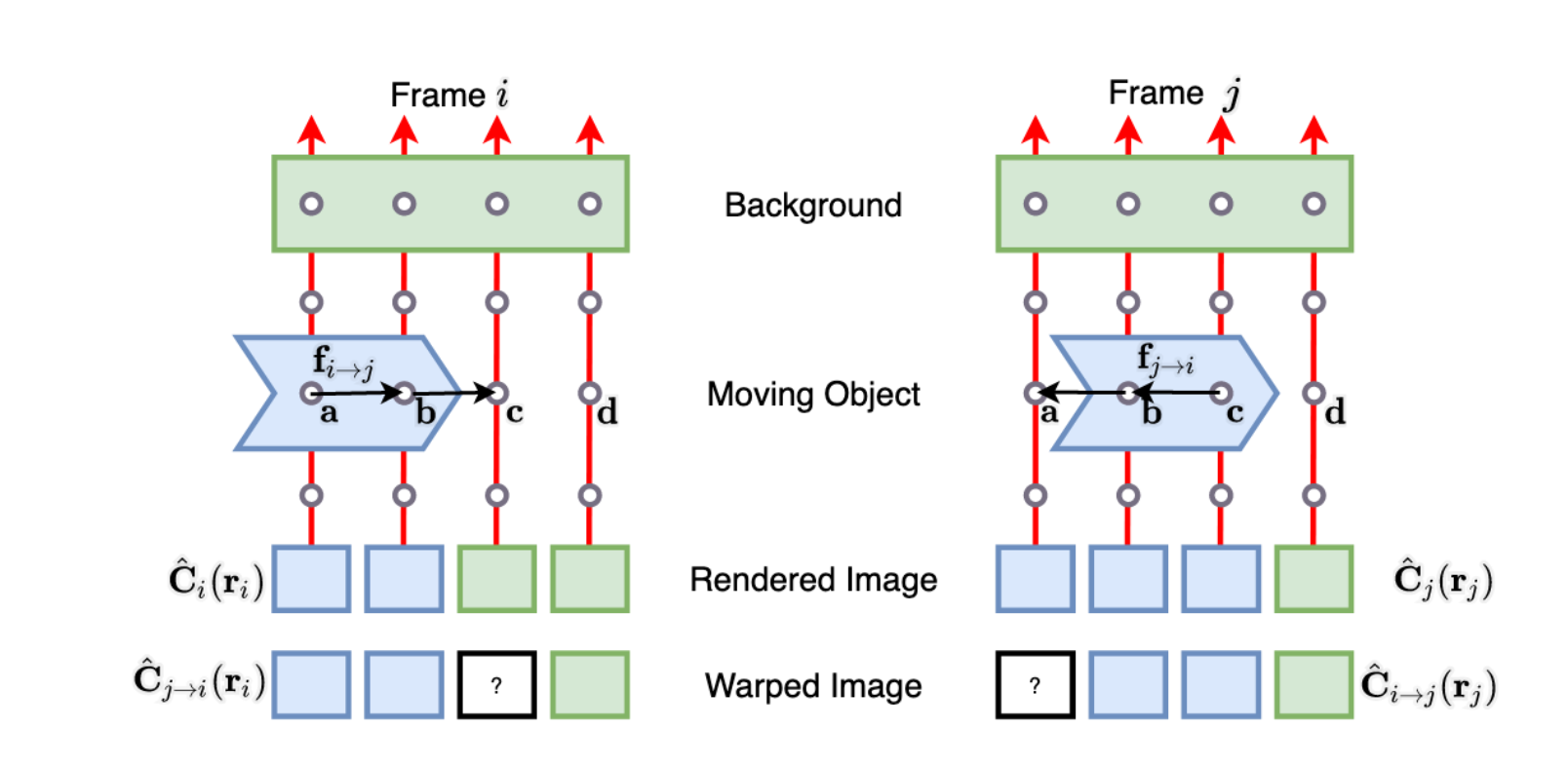
上図の通り、Scene Flowを用いると、時刻における3次元表現を時刻にワープさせることができ、時刻におけるピクセルの色になります。そのため、とが一貫しているという仮定を置くことができます。 しかし、この一貫性は、オクルージョンなどにより、物体の境界で曖昧になることがあります。下図(論文中 Fig. 3)を見てください。一番下のワープさせた画像(Warped Image)では、実際の画像(Rendered Image)と一致しない部分(?の部分)が発生しています。 この曖昧さに起因するエラーを軽減するため、Scene Flowに対応する重みを追加で予測するようにしています。この重みは、最適化時に、輝度一貫性のエラーをどの程度の強さで適用すべきかという情報を与えます。
-
サイクル一貫性
時刻で予測されたScene flow は、時刻におけるScene flow に対応します。そのため、時刻の3次元点に対するScene Flow と 時刻の点をScene Flowでワープさせた点 に対するScene flow は対応したベクトルであるため(向きは逆)、が小さいほど、一貫性があることになります。 -
幾何学的整合性
この幾何学的整合性は、三次元再構成の分野では、よく適応される手法で、隣接するフレーム間の正確な対応関係を構築します。 例えば、隣接したフレーム間のピクセルの移動量をオプティカルフローで計算するとします。この時、ピクセルの関係が成り立ちます。一方で、別ルートでこのピクセルの推定値を計算することができます。まず、scene flow と上を通る3次元点を計算し、に射影した点を2次元ピクセルに変換するとが計算できます。これらの誤差は、再投影誤差と呼ばれ、良く使用されています。また、安定性のため単視点深度項も設けられています。この項は、別途用意した単眼深度推定ネットワークにより推定された深度と、予測した密度から計算される深度の差を考えています。
この幾何学的整合性はノイズが多い(試した動画でもノイズが多かった)ため、学習の初期化のみに使用され、学習中は重みを0にして無視しています。
静的なシーン表現との統合
上記のScene Flow Fieldを用いることで、動的な画像群に対して、最先端の性能になります。しかし、静的なシーンにおいて、以前のNeRFを用いて表現した方が性能が向上することが論文内で示されています。そこで、各ピクセルにおいて、多層パーセプトロンを用い、動的なシーン表現(色、密度)と静的なシーン表現、これらのブレンド率を出力し、線形補間的に統合することが提案されています。もし、動的な部分の場合、動的なシーン表現が大きな割合で割り当てられ、一方で静的な部分の場合、静的なシーン表現が割り当てられます。
時間情報の補正
動的なシーンの場合、時刻との間の情報を補間する必要があります。基本的には、3次元点で線形補間されます。すると、時刻の色と密度表現は、時刻, の色と密度表現を、で変異させ、, の割合でブレンドしたものになります。
まとめ
最後に、実際の比較画像(論文中Fig.8)を示します。明らかに破綻が少なく、動的なシーンも表現できています。NSFFも含めNeRFは、比較的に新しい分野で、まだまだ研究すべき部分はたくさんあります。例えば、今回、試した際の学習に4日ほどかかりました。たった、数秒の表現を学習するためにこれだけ時間がかかるのは、大きな欠点だと思います。しかし、KiloNeRF: Speeding up Neural Radiance Fields with Thousands of Tiny MLPsのように学習速度を早くする研究が行われていたり、汎用的にする研究なども行われています。今後、この研究が進むことで、ゲームのように好きな視点で、見たい風景を見る日が来ると思います。

