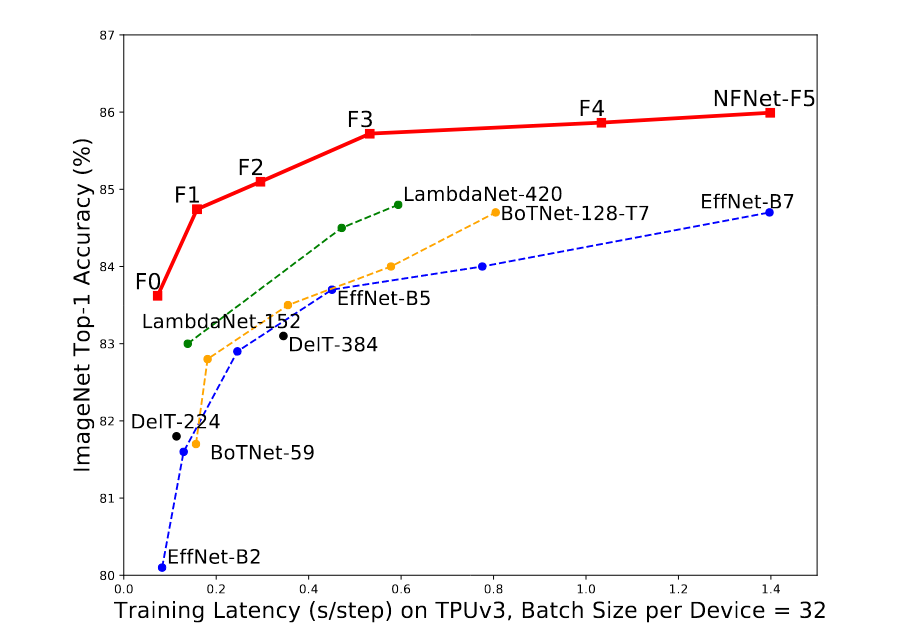
バッチ正規化の利点と欠点

深層ニューラルネットワークは、モデルの層が深くなったときにうまく学習できないという欠点があります。それを解決するため、ミニバッチ内における各チャネルの平均と分散を0, 1に正規化するバッチ正規化が開発されました。

バッチ正規化は、以下のような利点があり、現在、深層学習において良く用いられる手法の一つとなっています。

1. 残差部のダウンスケール
   Residual Networkの残差部における活性化のスケールを小さくすることができ、学習初期により良い勾配を持ちやすくなり効率的な最適化が可能になります。 Batch Normalization Biases Residual Blocks Towards the Identity Function in Deep Networks
2. 平均シフトの除去
   ReLUやGeLUのような活性化関数は非対称でかつ、平均が0ではないため、層の深さが増すにつれ、活性化間の内積が大きな値になる平均シフトが発生します。バッチ正規化を用いることで、各チャネルの活性化の平均が0になることが保証され、平均シフトを取り除くことができます。
3. 正則化の効果
   訓練データから計算されるバッチ統計量におけるノイズにより、テスト精度の向上が期待できます。
4. 効率的な大きなバッチサイズ学習
   バッチサイズが大きい時、損失面が平滑化され、より大きく安定した学習率、より少ないパラメータ更新による学習ができます。

一方で、以下のように、実用的な欠点があると指摘されています。

1. 処理のために高価な操作が必要で、勾配を評価するのに必要な時間が大幅に増加することがある
2. 訓練中と推論時のモデルの挙動が不一致になることがあり、調整するために別途ハイパーパラメータを導入する必要がある
3. ミニバッチにおける学習データ間で特立性を保てない

上記のような欠点を取り除きつつ、利点だけを活かしたいというのが、本論文のモチベーションです。

バッチ正規化を取り除くためのNormalizer-Freeのモデルとは

バッチ正規化を取り除きつつ、精度良く学習する取り組みとして、CHARACTERIZING SIGNAL PROPAGATION TO CLOSETHE PERFORMANCE GAP IN UNNORMALIZEDRESNETSという研究が行われていました。上記の論文では、Normalizer-Free ResNets (NF-ResNets)というモデルが提案されています。

下図(論文中Figure 5, 6.)がこのモデルの重要な部分(NFBlock)です。左がTransition-Block, 右が、Non-Transition Blockと呼ばれます。

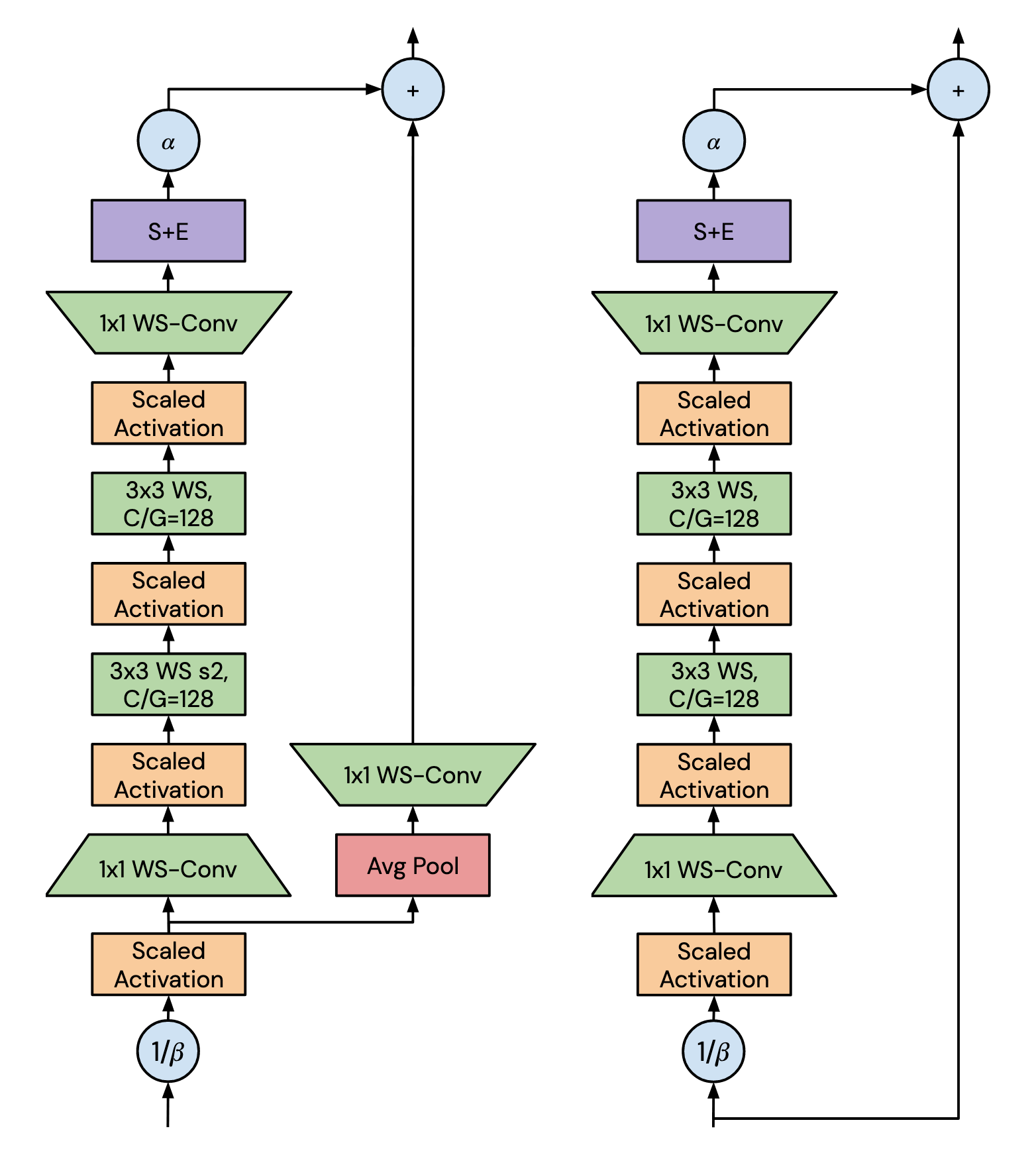
このNFBlockでは、以下のような工夫が行われています。

1 . 残差ブロック

このモデルは、残差ブロック機構となっており、

$h_{i+1} = h_i + \alpha f_i (h_i / \beta_i)$

で表されます。ここでは、$h_i$がi番目の残差ブロックの入力、$f_i$が$i$番目の残差ブロックにおける計算を行う関数です。 $f_i$は、$var(f_i(z)) = var(z)$のような制限を設けることで、分散を保持しています。

$\alpha$を活性化の分散を増加させる割合とし、$beta$を$i$番目の残差ブロックの分散$\beta_i = \sqrt{var(h_i)}$とすると、$var(h_{i+1}) = var(h_i) + \alpha^2$となります。ここで、上図のように$\beta$を用いて、ダウンスケール($h_i / \beta_i$)させると、$var(h_{i+1}) = 1 + \alpha^2$になることが期待されます。

また、$\alpha$に対して、0に初期化し、学習する対象に含めるSkipInitという工夫も行われています。

2. Squeeze-Excite (S+E)

Squeeze-Excite、畳み込み層の各チャネルに適応的な重みをかけることで、より性能が良いモデルにする仕組みです。 簡単に書くと、以下のような処理を行っています。

out = GlobalAvaragePooling(input) 
out = Linear(Activation(out))
out = Sigmoid(out)
out = out * input

Scaled Weight Standardization (SW)

この手法は、畳み込みレイヤーで、正規化することで、再パラメータ化を行っています。

$\hat{W_{ij}} = \frac{W_{ij} - \mu_i}{\sqrt(N) \sigma_i}$

ここでの$W_{ij}$は重みで、$\mu_i$、$\sigma_i$は重みの平均、分散です。Nは、fan-in(入力数)です。

活性化関数のスケーリング

NFNetsでは、活性化関数として、GeLUを使用していますが、出力の分散を1にするためにスケーリングしています。

例えば、論文の実装では、以下のようにしています。

F.gelu(input) * 1.7015043497085571

Stocastic Depth

上記の残差ブロックを確率的にドロップさせることで、学習時間の向上や勾配消失を防ぐことができます。 例えば、以下のようにして訓練時に、inputを確率的にdropさせることができます。

keep_prob = 0.5
if training:
    out = floor(random_int + keep_prob) * input

いろいろ工夫したけど...

以上のNFBlockを踏まえて、モデルを簡単に書くと以下のようになります。

out1 = stem(input)
out_n = [NFBlock(out1), NFBlock(out2), ...]
out = classifier(out_n)

stemは、畳み込み層からなる局所特徴量を抽出するブロックで、残差機構などは導入されていません。 NFBlockの最初のものだけTransition-Blockの構造で、他はNon-Transition-Blockです。Transition-Blockは、チャンネル数を増加させる機能があります。

結果として、上記の研究であるNF-ResNetsは、バッチサイズが2048までのImageNetに対する性能で、バッチ正規化 + ResNetと同等でした。しかし、4096以上のバッチサイズで急激に性能が劣化しています。また、EfficientNetsほどの性能が出ていないという問題もありました。

適応的勾配クリッピング(AGC)を用いた学習

上記のように、バッチサイズや単純な性能という点で問題があるNormalizer-Freeな手法ですが、論文では、適応的勾配クリッピング(AGC)を導入することで、解決しました。

この手法は文字通り、

1. 学習時の重みの勾配が大きい時にクリッピングする
2. クリッピングする値を適応的に決める

というものです。

式にすると以下のようになります。

$G_i^l \rightarrow \left\{ \begin{array}{ll}\lambda \frac{||W_i^l||_F}{||G_i^l||_F}G_i^l & if \frac{||W_i^l||_F}{ ||G_i^l||_F} > \lambda \\G_i^l &(otherwise)\end{array} \right.$

あるレイヤ$l$のi番目のパラメータを$W_i^l$、勾配を$G_i^l$とし、そのフロベニウムノルム( $||*||_F$)の比率を計算することで、学習時に重みがどのくらい変化するのかという情報を適応できるようになります。

例えば、比率が大きい時、学習が不安定になりやすいため、勾配をクリッピングすることで、学習を安定させる効果があると考えられます。

簡単に処理を書くと、以下のようになります。この処理は、Optimizerにて実行されます。

param_norm = max(unitwise_norm(input), eps) # norm計算
grad_norm = unitwise_norm(intpu.grad()) # norm計算

# クリッピングする勾配を選択 
#ここでは、lambdaを使用せず、比率が1を超えるものをクリッピンするようにしている
trigger = grad_norm > param_norm 

# クリッピンした勾配を計算
clipped_grad = input.grad() * (param_norm / max(grad_norm, 1e-6)) 

# triggerで選択されたものは、clipped_gradから選択される。
# そのほかは、input.gradから選択される
out = where(trigger, clipped_grad, input.grad()) 

実験の結果

実験の結果、一番上の性能図のような凄まじい結果が得られており、また、大きなバッチサイズでも学習ができていました。 ここでは、クリッピングする値$\lambda$の設定も重要で、値が十分に小さい時に学習がうまく行っていました。

AGCの適用に関する結果として、モデルの最終層(classifier部分)に適用すると性能が劣化していたことから、classifierには、AGCを適用しないほうが良さそうです。

まとめ

機械学習における画像処理でデファクトスタンダードになっているResNetsやEfficientNetsは、画像分類だけでなく、物体検出など多くのタスクで使用されています。今回の論文のように簡単な仕組みで精度良く学習可能なモデルが出てきたことで、今後、他のタスクにも使用され、より良い性能が出ることが証明されると嬉しいです。

また、AGCの仕組みは、Optimizerにて行われるので、他のモデルにも適応できないかと思います。

今年も、本論文やAttention機構の導入など、画像処理において、大きな進歩がある年であることが期待できます。

参考

deepmind-research/nfnets at master · google-deepmind/deepmind-research

This repository contains implementations and illustrative code to accompany DeepMind publications - google-deepmind/deepmind-research

github.com