今までのSiamese Learningとの違い

下図(論文中 Fig.3)は、論文にて提案されているSimSiamと、代表的なSiamese学習を用いた表現獲得の手法を示しています。 各手法は、下図の2つのencorderの出力を、それぞれ$z_1$, $z_2$とした時、$z_1 = z_2$に収束してしまうという崩壊問題に対して、様々な方法で対処しています。 崩壊問題がなぜ、問題であるかというと、ここでは類似度を学習したいわけではなく、画像の表現を学習したいためです。

以下、SimSiam以外の各手法を簡単に説明します。

• SimCLR
  崩壊問題を解決するため、大量のネガティブサンプリング(対象と無関係なデータ)が必要で、様々な負例との比較を行うため、バッチサイズを大きくする必要があります。実際、論文中でもバッチサイズが4096や8192など大きなバッチサイズで、良好な精度を達成していました。しかし、この手法は、各encoderに入力している拡張した画像同士の類似度を近くしているだけで、表現を学習しているわけではありません。
• BYOL
  momentum encorderの導入と、stop gradientによる勾配伝搬の停止によりパラメータ更新の停止により、ネガティブサンプリングと崩壊の問題を解決しています。しかし、momentum enconderは、勾配停止により学習されないため、encoderのパラメータとmomentum encoderのパラメータを適当な割合で足し合わせて更新する必要があり、実装が複雑になります。
• SwAV
  この手法は、崩壊問題に対して、クラスタリングを用いて、対処しています。具体的には、各encoderの出力とクラスタベクトルとの類似度を取り、Sinkhorn-Knoppアルゴリズムを用いて最適化したクラスタ割当確率と、Softmaxから得られるクラス割当確率が一貫していることを仮定して問題を解いています。(詳細は、この記事がわかりやすかったです。) この手法も、ネガティブサンプリングの問題を解決していますが、実装が複雑です。

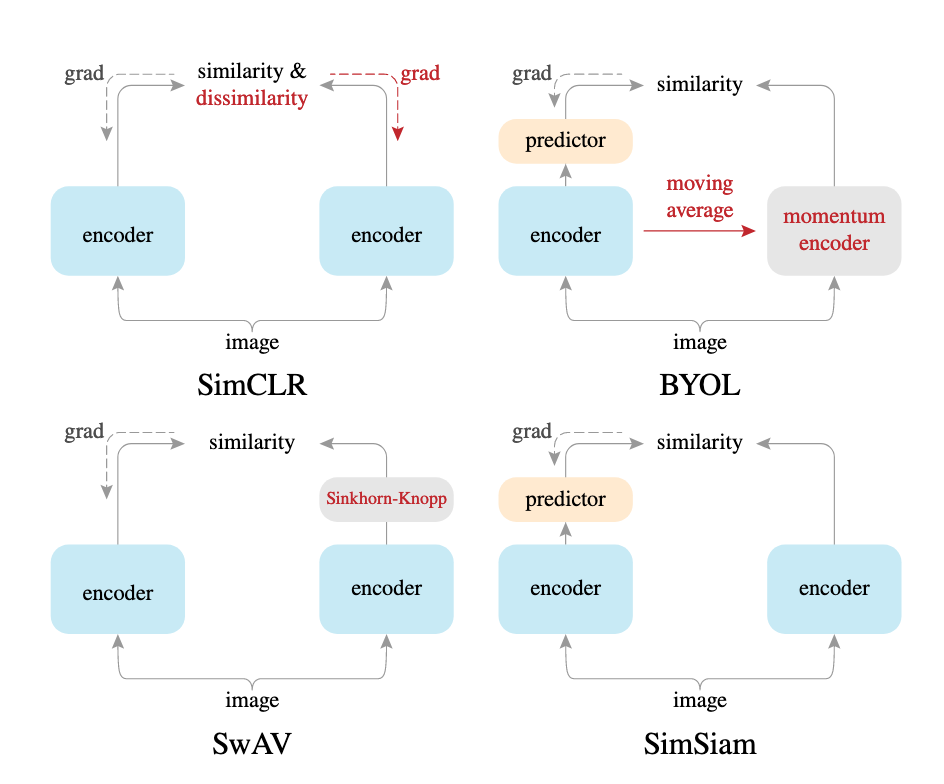
上記のように、これまでの手法は、ネガティブサンプリングを行い必要なデータが増える、または、momentum encoderやクラスタリングを行い実装が複雑なるなどの問題がありました。そこで、提案されたのが、SimSiamです。これは、ネガティブサンプリングが必要なく、stop gradient(勾配停止)と、予測レイヤを追加するのみで、以下の疑似コードのように簡単に実装可能です。ここでは、予測レイヤ(h)を導入しており、また、損失(D)の中では、detachを使用して、勾配計算を止めています。

論文の結果を見ると、既存の手法より良い結果を示していました。この理由を、勾配停止と、予測モデルにあるとしており、実際、勾配停止がない場合と予測レイヤーがない場合の実験で、大きく精度が低下していました。

なぜ、勾配停止と予測モデルが必要なのかの仮説

表現学習の損失を定式化すると、以下のように書くことができます。

$\mathcal{L}(\theta, \eta)=\mathbb{E}_{x, \mathcal{T}}\lbrack||\mathcal{F}_{\theta}(\mathcal{T}(x)) - \eta_x||^2_2\rbrack$

ここで、$\mathcal{F}$は、パラメータ$\theta$で定義されたニューラルネットワークで、$\mathcal{T}$はAugmentation(データの拡張)、$x$は画像です。 $\eta$は、画像$x$の特徴表現で、最終的には、あらゆるデータ拡張の平均で更新されていきます。ここでの目的は、画像の表現を出力する、ネットワーク$\mathcal{F}_{\theta}$を学習することです。しかし、$\rm{min}_{\theta, \eta} (\mathcal{L}(\theta, \eta))$のように損失を最小化するためには、ネットワークを学習するだけでなく、特徴表現$\eta$も学習する必要があります。

そこで、EMアルゴリズムのように、以下のように更新することで、この損失を最小化しています。

1. $\eta$を固定し、損失が最小となる$\theta$を計算
   $\theta^t \leftarrow \rm{arg min}_{\theta} \mathcal{L}(\theta, \eta^{t-1})$
2. $\theta$を固定し、損失が最小となる$\eta$を計算
   $\eta^t \leftarrow \rm{arg min}_{\eta} \mathcal{L}(\theta^{t}, \eta)$

これらの計算を繰り返すことで、$\mathcal{L}(\theta, \eta)$を最小化することができます。

まず、2.から考えていきます。$\eta^t$の更新は表現学習の損失より、$\eta^t_x \leftarrow \mathbb{E}_{x, \mathcal{T}}\lbrack\mathcal{F}_{\theta^t}(\mathcal{T}(x))\rbrack$で計算できます。これは、データ拡張に関する分布における画像$x$の平均的な表現を割り当てていることになります。

しかし、データ拡張に関する分布は未知であるため、実際にこれを計算することは困難です。

SimSiamにおける近似

そこで、SimSiamでは、期待値計算をせず、以下の式で$\eta$を更新するように近似しています。これは、適当な一回のサンプリングによる画像とデータ拡張で更新していることになります。

$\eta^t_x \leftarrow \mathcal{F}_{\theta^t}(\mathcal{T}(x))$

また、この結果、$\theta$の更新も以下のようになります。この式は、一般的なSiamese学習の使用する定理ですね。

$\theta^{t+1} \leftarrow \rm{arg min}_{\theta} \mathbb{E}_{x, \mathcal{T}}\lbrack||\mathcal{F}_{\theta}(\mathcal{T}(x)) - \mathcal{F}_{\theta^t}(\mathcal{T'}(x))||^2_2\rbrack$

さて、上の$\theta$を更新する式では、片方のネットワークのパラメータは定数($\theta^t$)で固定されています。つまり、SimSiamでは勾配停止を適用することになります。

一方で、SimSiamの近似により、表現学習の損失に対するEMアルゴリズムライクな更新とのギャップが発生しています。それは、$\eta$の計算時に、期待値計算を除去したことです。 この期待値計算を補助するために、予測レイヤー$h$を導入しています。各ネットワークの出力を$z_1, z_2$とした時、予測レイヤの出力$h(z_1)$は、$z_2$との誤差が最小となることがゴールになります。これは、任意の画像$x$に対して、$h(z_1)=\mathbb{E}_z\lbrack z_2 \rbrack = \mathbb{E}_{\mathcal{T}} \lbrack f(\mathcal{T}(x)) \rbrack$を満たす$h$を計算することになり、画像の特徴表現$\eta$の更新式になります。この$h$は実際に期待値を求めるわけではありませんが、論文では、この予測レイヤを用いることで、近似によるギャップを埋めてくれるのではないかと仮定していました。

まとめ

上記のように、順序だって学習のアーキテクチャを作ることは、憧れます。そして、実際に性能が出ていることも、すごいと思います。 SimSiamは、実装も簡単なので、今後、Siamese学習を行う際には、使用も検討に入れて良いのではと思います。 論文中には、他にも、パラメータに関する考察や比較実験があり、面白いので是非読んでみてください。