GNNによる制約なし二次最適化問題へのアプローチ

参考

今回の内容は、[[2107.01188] Combinatorial Optimization with Physics-Inspired Graph Neural Networks](https://arxiv.org/abs/2107.01188)を参考・解説したものです。

コードはこちらです。

GitHub - amazon-science/co-with-gnns-example

Contribute to amazon-science/co-with-gnns-example development by creating an account on GitHub.

github.com

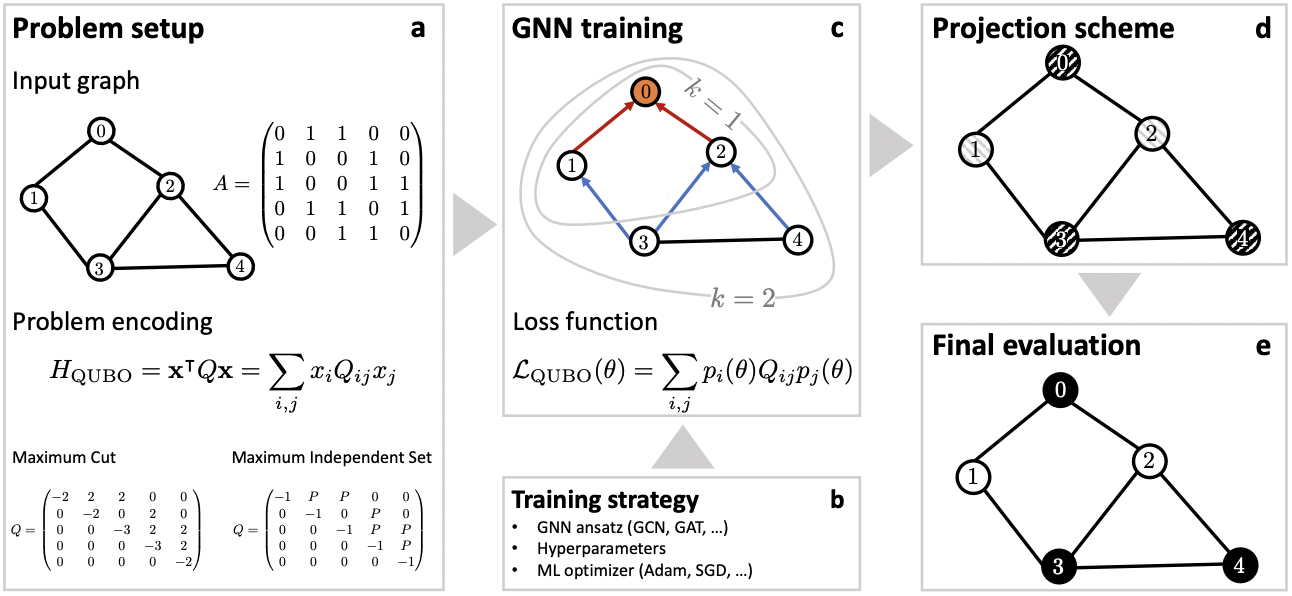
アルゴリズム概要

まず、最適化問題を二値の決定変数$x_ν∈ \{0,1\}$からコスト関数Hを定義するため、この変数を無向グラフ$G=(V,E)$の隣接行列へ対応づけます。

次に、これをQUBO形式の問題へ変換し、Q行列を決定します。

各ノードの重みが1だとして、MaxCut問題であれば、以下になります。

ネットワークの最終層にはsigmoidを介して、各ノードに与えられるパラメータ$\theta$に対して$p(\theta) \in [0,1]$が与えられます。

GNNの損失関数には、QUBOと対応付けるため、このQ行列と、$p(\theta) \in [0,1]$を使って以下のようになります。

パラメータの更新後はround関数などで、各ノードに与えられている$p(\theta) \in [0,1]$を$\{0,1\}$に割り当てて次ステップへといった流れです。

アルゴリズムの詳細と結果

詳細については、実装しつつみていきます。

まず、ネットワークは単純な２層のGraphConvを利用します。

class GCN_dev(nn.Module):
    def __init__(self, in_feats, hidden_size, number_classes, dropout, device):
        super(GCN_dev, self).__init__()

        self.dropout_frac = dropout
        self.conv1 = GraphConv(in_feats, hidden_size, activation=torch.relu).to(device)
        self.conv2 = GraphConv(hidden_size, number_classes, activation=torch.sigmoid).to(device)

    def forward(self, g, inputs):
        # input step
        h = self.conv1(g, inputs)
        h = torch.relu(h)
        h = F.dropout(h, p=self.dropout_frac)

        # output step
        h = self.conv2(g, h)
        h = torch.sigmoid(h)

        return h

最終的にsigmoidを通して、グラフ表現を$[0,1]$で、出力しています。

今回は最終的に、(h.detach() >= 0.5) * 1で、$\{0,1\}$へマッピングさせます。

次に損失関数です。

def loss_func(probs, Q_mat):
    probs_ = torch.unsqueeze(probs, 1)

    # minimize cost = x.T * Q * x
    cost = (probs_.T @ Q_mat @ probs_).squeeze()

    return cost

この損失関数は、Q行列を問題によって変えることで機能させられます。

具体的にMaxCut問題を使って、GNNを学習させてみます。

まずは、Q行列を定義します。

# nx_graph: graph as networkx object

n_nodes = len(nx_graph.nodes)

Q_mat = torch.zeros(n_nodes, n_nodes)

for (u, v) in nx_graph.edges:
    Q_mat[u, v] = 2

for u in nx_graph.nodes:
    Q_mat[u, u] = -nx_graph.degree[u]

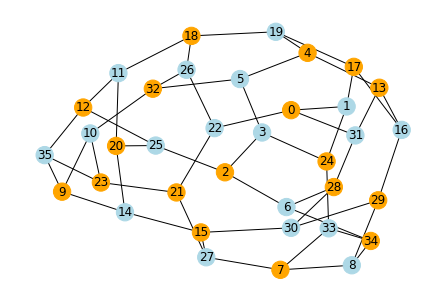
今回グラフは36nodeと3degreeのグラフを考えます。

nx.random_regular_graph(d=3, n=36, seed=random_seed)

学習結果は以下のようになります。

Running GNN...
Epoch: 0, Loss: -0.1906130313873291
Epoch: 1000, Loss: -5.387984275817871
Epoch: 2000, Loss: -23.445919036865234
Epoch: 3000, Loss: -36.0899658203125
Epoch: 4000, Loss: -42.25738525390625
Epoch: 5000, Loss: -45.481563568115234
Epoch: 6000, Loss: -47.31055450439453
Epoch: 7000, Loss: -48.44272232055664
Epoch: 8000, Loss: -49.12056350708008
Epoch: 9000, Loss: -49.50899887084961
Epoch: 10000, Loss: -49.726173400878906
Epoch: 11000, Loss: -49.8489875793457
Stopping early on epoch 11013 (patience: 100)
GNN training (n=36) took 46.418
GNN final continuous loss: -49.850135803222656
GNN best continuous loss: -49.850135803222656

Independence number found by GNN is 18 with 2 violations
Took 46.483s, model training took 46.465s

コードについては、co-with-gnns-example/gnn_example.ipynb at main · amazon-research/co-with-gnns-example · GitHubでもっと詳細に書かれていますので、こちらを参照してください。

最適化ソルバーとの比較

数値実験として、他の最適化ソルバーとの比較をします。

今回のGNNのソルバーとの比較を最後のカラムに記載してあります。

他のソルバーと約1%程度のエラーであることがわかりました。

また、数百ノードのグラフの場合、GNNソルバーが従来のソルバーと同等（またはそれ以上）のパフォーマンスを発揮できることが報告されています。

n≈104〜106ノードの大きなグラフの場合、今回のアプローチは、次数が3、5に対して精度の高い近似を得られるそうです。