shimao

変分推論によるベイズロジスティック回帰をPythonで実装する

#machine-learning #bayesian inference #logistic regression

2019/08/23

Table of Contents

本記事の対象者
ベイズ推論？ロジスティック回帰？
実装
推論結果
実装について補足説明
実装してみての感想
余談：輪読会の形式・進め方についてと感想
参考リンク

本記事の対象者

機械学習に興味がある方
ベイズ推論に興味がある方

ベイズ推論？ロジスティック回帰？

ここでは簡単に説明させていただきます。

（詳細が知りたい方はぜひ書籍を読んでみてください。本当にわかりやすく、オススメです！）

ベイズ推論とは

wikipediaによると

ベイズ推定（ベイズすいてい、英: Bayesian inference）とは、ベイズ確率の考え方に基づき、観測事象（観測された事実）から、推定したい事柄（それの起因である原因事象）を、確率的な意味で推論することを指す。モデルのパラメータの事後分布を求めることで、未知の入力値

機械学習の様々な問題に適用出来る手法です。書籍には具体的な応用例として以下の事柄が紹介されていました。

次元削減・画像圧縮・画像欠損値の補完・時系列データの異常検知・スペクトログラムの分解・文章の分類・推薦システム

以下のQiitaなども概要を理解するのに良いかと思います。

5分でスッキリ理解するベイズ推定

ロジスティック回帰とは

分類問題において、分類される確率を求めるモデルです。

こちらのサイトの以下の説明文が内容を掴むのにわかりやすいと思いました。

ロジスティック回帰とは、例えば「その人の購入履歴」から、「この人が次にこの商品を買うかどうか」のような２値の予測を行うアルゴリズムです。

今回実装するのはベイズ推定を使ったロジスティック回帰です。

入力変数xのラベルyを推定するモデルのパラメータWの（近似）事後分布を求め、それをつかって未知の入力変数のラベルを予測できるようにします。

実装

入力変数xは2次元としています。以下、JupyterNotebookで実行する想定の実装となっています。

import math
import matplotlib.pyplot as plt
import numpy as np
import sys
from scipy.stats import bernoulli

np.random.seed(1234)

# xの次元数
M = 2

# xのデータ数
N = 25

# 変分パラメータの学習率
alpha = 1.0e-4

# 変分推論の繰り返し回数
max_iter = 20000

# xの事前分布の共分散行列Σ
Sigma_w = 100.0 * np.eye(M)

X = 2 * np.random.rand(M, N) - 1.0

W_truth = np.random.multivariate_normal(np.zeros(M), Sigma_w)

def sigmoid(a):
    s = 1 / (1 + math.exp(-a))
    return s

W_truth_tr = W_truth.T

Y = np.array([bernoulli.rvs(sigmoid(np.dot(W_truth_tr, X[:, i]))) for i in range(N)])


#一回図にして確認する
x1min = 2*min(X[0,:])
x1max = 2*max(X[0,:])
x2min = min(X[1,:])
x2max = max(X[1,:])

plt.figure()
plt.scatter(X[0, Y==1].T, X[1, Y==1].T, c="r")
plt.scatter(X[0, Y==0].T, X[1, Y==0].T, c="b")
plt.xlim([x1min, x1max])
plt.ylim([x2min, x2max])
plt.title("samples")
plt.show()

# 変分推論
def VI(Y, X, M, Sigma_w, alpha, max_iter):

    def rho2sig(rho):
        return np.log(1 + np.exp(rho))
    
    def calc_d_mu(Y, X, Sigma_w_inv, mu, rho, W):
        # 第一項は0なため不要
        term2 = np.dot(Sigma_w_inv, W)
        term3 = 0
        W_tr = W.T
        term3 = sum([ -(Y[i] - sigmoid(np.dot(W_tr, X[:, i]))) * X[:, i] for i in range(n)])

        return term2 + term3

    # diag gaussian for approximate posterior
    m, n = X.shape
    mu = np.random.randn(m)
    rho = np.random.randn(m)
    Sigma_w_inv = np.linalg.inv(Sigma_w)
    
    for i in range(max_iter):
        # sample epsilon
        ep = np.random.randn(m)
        W_tmp = mu + rho2sig(rho) * ep

        # calculate gradient
        d_mu = calc_d_mu(Y, X, Sigma_w_inv, mu, rho, W_tmp)
        d_rho = ((d_mu * ep) - (1 / rho2sig(rho))) * (1 / (1+np.exp(-rho)))

        # update variational parameters
        mu = mu - alpha * d_mu
        rho = rho - alpha * d_rho 

    return mu, rho

mu, rho = VI(Y, X, M, Sigma_w, alpha, max_iter)

def visualize_contour(mu, rho, X, Y):
    N = 100
    R = 100
    x1min = 2*min(X[0, :])
    x1max = 2*max(X[0, :])
    x2min = min(X[1, :])
    x2max = max(X[1, :])

    x1 = np.linspace(x1min, x1max, num=R)
    x2 = np.linspace(x2min, x2max, num=R)
    x1grid = np.tile(x1, (R,1))
    x2grid = np.tile(x2, (R,1)).T
    val = np.array([x1grid.flatten(), x2grid.flatten()])
    
    z_list = []
    W_list = []
    sigma = np.log(1 + np.exp(rho))

    for n in range(N):
        W = np.random.multivariate_normal(mu, np.diag(sigma**2))
        z_tmp = [sigmoid(np.dot(W.T, val[:, i])) for i in range(N*N)]
        W_list.append(W)
        z_list.append(z_tmp)

    z = np.mean(z_list, axis=0)
    zgrid = np.reshape(z, (R, R))

    # precition
    plt.figure("contour")
    plt.contourf(x1grid, x2grid, zgrid, alpha=0.5, cmap="bwr")
    plt.scatter(X[0,Y==1], X[1,Y==1], c="r")
    plt.scatter(X[0,Y==0], X[1,Y==0], c="b")
    plt.xlim([x1min, x1max])
    plt.ylim([x2min, x2max])
    plt.title("prediction")
    plt.show()

    # parameter samples
    plt.figure("samples")
    for n in range(10):
         draw_line(W_list[n], x1min, x1max)
                         
    plt.scatter(X[0,Y==1].T, X[1,Y==1].T, c="r")
    plt.scatter(X[0,Y==0].T, X[1,Y==0].T, c="b")
    plt.xlim([x1min, x1max])
    plt.ylim([x2min, x2max])
    plt.title("parameter samples")
    plt.show()

def draw_line(W, xmin, xmax):
    y1 = - xmin*W[0]/W[1]
    y2 = - xmax*W[0]/W[1]
    plt.plot([xmin, xmax], [y1, y2], c="k")

visualize_contour(mu, rho, X, Y)

推論結果

以下の図は、2次元の入力変数xを各次元の値を横軸・縦軸に取ったグラフです。点の色は正解ラベルyに対応しています。色分け部分がロジスティック回帰モデルの推論結果で、各ラベルである確率分布を表しています。（そのラベルである色が濃い程確率が高い）

観測済みのデータ分布に応じて、確率分布が変化している様がわかるかと思います。

推論結果

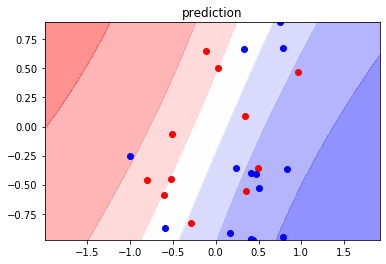
以下の図は、同じくxを横軸・縦軸に取ったグラフに、得られた事後分布からパラメータWを10個サンプルし、二値分類線を引いた図となります。

二値分類線

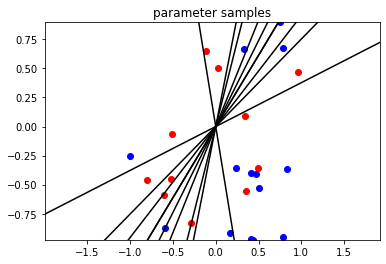
実装について補足説明

大まかな流れは以下となります。

観測済みデータとして入力変数xとラベルyを生成。
変分推論にて変分パラメータμとσを更新。
得られた変分パラメータを使ってWをサンプルし、グラフ空間中のXに対して分類確率を計算して描画する。

著者のサンプルコードから大きく変えたのは一点だけでして、変分パラメータの勾配算出の計算過程を変えています。（書籍の数式を出来る限りそのまま使っています。）以下、変分パラメータの勾配計算部分の数式を記載します。

申し訳有りませんが、上記の導出を書き出すとすごく長くなってしまうのでほぼ結論だけ書いてます。Wの事後分布と近似事後分布のKLダイバージェンスの最適化による導出可能です。

※λはWの事前分布の分散の逆数（共分散行列Σの逆行列）です。

※εは平均０、分散1のガウス分布に従う値です。wに再パラメータ化トリックを使い、得られます。

上記の勾配の計算式をそのまま適用しています。（著者のサンプルコードでは最終的な勾配の値は一致するものの、計算過程が異なるようです。もしかすると計算効率対策？かもしれません）

実装してみての感想

実装してみて動かしてみて初めてちゃんと理解できた気がします。
- 数式の導入を目で追って理解できたつもりになっていましたが、実際に手で書き下そうとすると理解しできていない部分が明らかになったりして、やはり理解が深まります。
- 微分公式を忘れていたりしていて、悲しい気持ちになりました…。が、今回かなり思い出すことが出来たので良かったです。やっぱり手を動かさないと忘れてしまいますね。
一方でどうしても時間がかかってしまうので、自分の場合は全てを実装してみるというよりはピンポイントで気になったモデルや理解が出来ているか不安なところだけを実装するのが良いのかなと思いました。
今回実装してみて理解が深まったので、今後はPyStan等の既存パッケージの使い方を勉強したいと思っています。
本筋とは関係ないですが、今回著者のサンプルコードを動かすためにJuliaを初めて触りました。
- 数値計算がかなり書きやす良いなぁと思いました。
- 一方、1.0以前・以後で書き方がガラッと変わっているのと（メジャーバージョンの変更なのでしょうがないですが）、書き方が直感的でない部分がある（ex. A'でAの転置行列）ので戸惑いました…。

余談：輪読会の形式・進め方についてと感想

メンバは4名で週２回、一回2-3時間で進めました。（メンバの出張等で中止の会もあったので実際は週1.5回くらいかも）
各自予習してくるスタイルで、進捗は一番遅い人には合わせず、下から2番目くらいの人に合わせる感じです。
予習の中でよくわからなかった点や思ったことを話す形で進めました。（なので、厳密には輪読ではないかも…。）
週2回は結構きつかったですが、まとめてガツッとやったことでダレずに最後まで行けたので良かったと思います。
輪読会が終わった後は1,2週間に１回集まって、本実装のような「こんなのやってみたよ」的な共有をする会を続けています。
個人的にあまり輪読会賛成派ではなかったのですが、今回の経験を経て俄然賛成派になりました。
- 元々「自分で勉強すればいい」と思っていたのですが、やってみてやはり１人でやるより格段に理解が深まりました。
- メンバ次第かもしれませんが、みんな楽しんでやっていたので大学のゼミみたいで面白かったです。
- 1人でやっていると忙しくて伸ばし伸ばしにしちゃって可能性も高かったと思います。